The movement of cells in the extracellular environment plays an important role in many biological events, such as tumour invasion or immune reaction. In order to move, cells have to apply forces on the extracellular matrix. Elucidating how the cells generate these forces and what effect this has on their environment can help us to understand these biological processes. As such, there has arisen recent interest in approaches that can measure these forces.
Herbert Levine and his team at Rice University (USA) and NRCN (Israel) have developed a computational model that predicts the behaviour of cells in complex fibrous environments. Their work pays special attention to the limitations that may arise when trying to compare this theory with experimental data, and possible next steps to overcome them (Phys. Biol. 15 026001).
How do we measure cell movement?
Cells normally reside in the extracellular matrix, an intricate 3D fibrous environment, and to move around they must pull and deform those fibres. By placing theoretical beads in these fibres, we can measure the matrix deformation and, in principle, determine the force that the cells are exerting on the surrounding components. However, the complexity of the extracellular matrix surrounding the cell makes such determination challenging; if one is not careful, the inferred forces, will not be representative of the actual values.
A motion-cell computational model
In this study, the authors employed a lattice-based mechanical model that is based on a network of repeated polygonal motifs, such as triangles. This 2D model is able to mimic the properties of the cellular environment (such as the nonlinear elastic response of fibres), has similar properties to 3D models and offers a high computational efficiency. In this model, simulations consisted of inserting a round cell into the lattice (triangle network) and imposing the interactions between them. Next, by employing validated equations that govern the model, the researchers used the observed deformations in the lattice to calculate the forces generated by the cell.
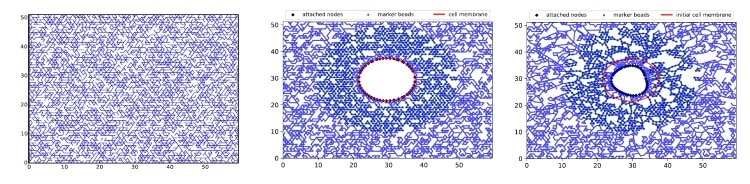
However, this is a complex inverse problem, even if we know the equations exactly, and hence some limitations appear during the determination of the desired parameters. For example, poor resolution (or distance between intersections receiving different amounts of force) can lead to inaccuracies.
In general, we can never know the exact equations for the actual system. For example, the model assumes that all the fibres of the lattice have similar properties (i.e., stiffness). However, this is not representative of the extracellular environment, which is comprised of fibres with different sizes and stiffness values. Another important limitation is that we must know the exact fibre geometry to determine the local mechanical properties for the inversion; typically, all we know is the macroscopic response, which is not sensitive to heterogeneity and microscopic structures. This could lead to high inaccuracies in the predictions.
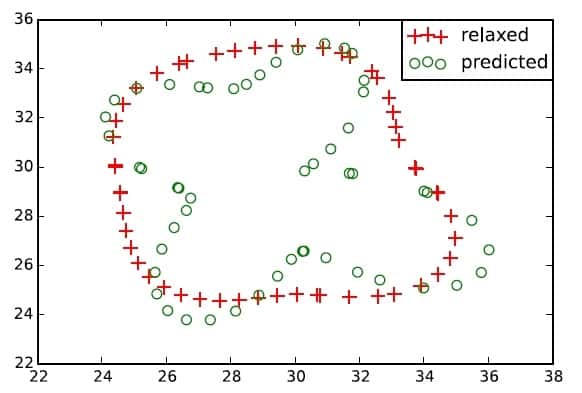
To overcome these hindrances, the authors propose to combine the standard approach, which tries to measure the traction forces from the lattice deformation, with another that also measures the mechanical responses of determined local beads (single points of the lattice). This approach would allow a more precise reconstruction of a specific piece of extracellular environment, and therefore, do a much better job in calculating the forces exerted on it. This challenging task will be part of the authors’ future work.